|
|
||||
|
A mágica dos juros compostos
O 'juro composto' é a maior invenção da humanidade, porque permite uma confiável e sistemática acumulação de riqueza. A Einstein
|
|
|||
|
Albert Einstein, opinava que 'a força mais poderosa do Universo não é a força da gravidade, mas sim, a força dos juros compostos!' Ele costumava se referir à ela como 'a mágica dos juros compostos'.
No excel* ou em uma calculadora pode-se descobrir o que impressionou o gênio: com taxas de juros de 15% ao ano uma dívida dobra em 5 anos, com 12% ao ano quase dobra em 6 anos e com 10% ao ano dobra em pouco mais de 7 anos.
Mas, afinal, o que são os juros compostos e como eles afetam nossa vida? Inicialmente, saiba que eles causam um tremendo dano para o devedor!
Quando você vê em uma propaganda: "Compre uma televisão à vista por R$ 1.000,00 ou a prazo por 5 parcelas de R$ 260,00" Você, distraído, pode pensar: "A prazo, pois prefiro pagar parcelado, em poucas vezes por mês, e em apenas 5 meses eu acabo de pagar."
Mas você esqueceu de pensar em um "detalhe": 5 parcelas de R$ 260,00 dá o equivalente a R$ 1.300,00 que é 30% a mais do que a oferta á vista (R$ 1.000,00). São em situações como essas que você percebe como a Matemática Financeira é uma ferramenta útil na análise de algumas alternativas de 'investimentos' em bens de consumo.
Sob a ótica do tomador do dinheiro seu efeito é fatal. Quando você paga ao banco a prestação contendo o principal e juros pactuados, ainda lhe são exigidos novos juros dos juros que você está pagando! Assim funciona!
Com juros compostos (capitalização acumulada) o montante cresce a cada período em progressão geométrica. Ao final de cada período de capitalização, o montante se torna capital para o período seguinte e assim por diante (juros sobre juros). Assim, a fórmula para o cálculo do Montante é:
M = C (1 + i )n
Onde: 'C' é o capital, 'i' é a taxa % e 'n' é o período de tempo.
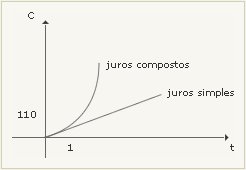
Com juros compostos após cada período, os juros são incorporados ao principal e passam, por sua vez, a render juros. Isso também é conhecido como "juros sobre juros". Abaixo um exemplo para ilustrar a diferença entre os crescimentos de um capital através de juros simples e juros compostos:
Suponha que R$ 100,00 são emprestados a uma taxa de 10% a.a. (ao ano):
Veja como fica a ilustração gráfica entre esses dois fenômenos matemáticos:
Agora a pergunta do Milhão: Já pensou em usar os juros compostos a seu favor?
O investimento em ações torna-se na prática uma forma de capitalização a juros compostos - ou previdência. Um investidor que aplica R$ 500,00 todo mês em compra de ações de ótimas empresas - por exemplo pibb11, consegue após 20 anos de aporte e rendimentos reais de 20% ao ano, o patrimônio final de R$ 1.219.428,19!
Em paralelo, é possível afirmar que nas últimas décadas o investimento em ações superou a marca de 20% reais média a.a.
Sendo assim, veja alguns exemplos do poder dos juros compostos para aplicações mensais em carteira de ações de boas empresas durante 20 anos e com rentabilidade média projetada de 20% a.a. liquidas de inflação:
R$ 100,00 todo mês => R$ 243.885,64 em 20 anos ou 240 meses. R$ 100,00 todo mês => R$ 616.587,08 em 25 anos ou 300 meses. R$ 300,00 todo mês => R$ 731.656,92 em 20 anos ou 240 meses. R$ 300,00 todo mês => R$ 1.849.761,23 em 25 anos ou 300 meses. R$ 500,00 todo mês => R$ 1.219.428,19 em 20 anos ou 240 meses. R$ 500,00 todo mês => R$ 3.082.935,38 em 25 anos ou 300 meses.
=> click para acessar a planilha de juros compostos em formato excel |
||||
|
InvestGraf Investment Coaching © 2015 Todos os direitos reservados |
||||